É possível treinar uma IA para prever a Mega-Sena? Um estudo sobre os limites do machine learning

Nota editorial

Esta pesquisa foge parcialmente do escopo usual da Datavion, que se concentra na análise e visualização de dados do mercado financeiro.

O objetivo deste estudo não é explorar apostas ou jogos de azar, mas investigar, de forma rigorosa, os limites do uso de estatística e machine learning em processos projetados para serem aleatórios.

A Mega-Sena foi escolhida como objeto de estudo justamente por representar um caso extremo: um sistema onde, em tese, não há estrutura temporal, dependência entre eventos ou variáveis explicativas observáveis.

Ao documentar esse experimento, buscamos responder a uma pergunta recorrente - “é possível treinar uma IA para prever sorteios?” - com dados, método e validação, em vez de opinião ou intuição.

Este trabalho deve ser lido como um estudo negativo: um resultado que confirma o que a estatística já antecipa, mas que ainda assim é frequentemente ignorado.

Entender onde a análise de dados falha é tão importante quanto entender onde ela funciona. É essa fronteira que esta pesquisa explora.

Para um contraste em um domínio com estrutura temporal, veja também: Regimes de mercado do Bitcoin.

Resumo

Este artigo investiga se técnicas de machine learning conseguem extrair sinal preditivo de sorteios da Mega-Sena. Usamos o histórico completo de concursos de 1996 a 2025, treinamos modelos até 2024 e avaliamos em 2025, além de um rolling backtest ano a ano (2000-2025) com múltiplas janelas de histórico. A avaliação compara um modelo simples de regressão logística com baselines claros (frequência, raras, recência e aleatório). Os resultados mostram médias de acerto muito próximas do esperado teórico para um processo aleatório, com ganhos raros e sem consistência estatística. Concluímos que, para este problema, a estatística confirma a ausência de sinal útil.

Palavras-chave: loteria, machine learning, backtest, bootstrap, aleatoriedade, avaliação temporal.

1. Introdução

Loterias são desenhadas para serem imprevisíveis. Ainda assim, a pergunta “uma IA pode prever sorteios?” aparece com frequência. Este artigo responde a essa pergunta com método e validação. O objetivo não é incentivar apostas, mas mostrar o limite prático do machine learning quando o processo subjacente é aleatório.

O foco aqui é rigor: separar treino e teste de forma temporal, comparar com baselines, e validar resultados ao longo de muitos anos. Um bom método deve falhar de forma clara quando não há sinal, e é isso que testamos.

2. Dados e preparação

• Fonte: API pública da CAIXA, um concurso por chamada.
• Período: 1996-03-11 até 2025-12-20 (2954 concursos).
• Limpeza: deduplicação e reparo de linhas concatenadas no JSONL.
• Padronização: CSV com 6 dezenas por concurso e metadados básicos.

2.1 Frequências históricas (1996-2025)

Números que mais saíram no período:

• 10 (345), 53 (336), 5 (322), 37 (321), 34 (320), 33 (316).

Números que menos saíram no período:

• 26 (243), 21 (246), 55 (255), 22 (263), 15 (264), 3 (273).

3. Metodologia

3.1 Formulação do problema

Cada concurso sorteia 6 dezenas entre 1 e 60. Para cada concurso de teste, o modelo gera um palpite com 6 dezenas. A avaliação mede quantos números do palpite aparecem no resultado real.

3.2 Features

Usamos uma janela de histórico com tamanho fixo (janela W). Para cada concurso, construímos um vetor com 60 valores: o número de vezes que cada dezena apareceu nos W concursos anteriores. Esse vetor serve como entrada do modelo.

3.3 Modelos e baselines

1. Modelo ML (regressão logística One-vs-Rest)

• Treina um classificador por dezena, com class_weight balanced.
• Gera probabilidade para cada dezena e seleciona as 6 maiores (top-6).

2. Baseline frequência

• Seleciona as 6 dezenas mais frequentes no treino e usa sempre.

3. Baseline raras

• Seleciona as 6 dezenas menos frequentes no treino e usa sempre.

4. Baseline recência

• Em cada concurso, escolhe as 6 dezenas com maior tempo desde a última aparição.

5. Baseline aleatório

• Escolhe 6 dezenas aleatórias sem reposição a cada concurso.

3.4 Métricas

• Média de acertos: média do número de acertos (0 a 6) por concurso.
• Distribuição de acertos: contagem de 0, 1, 2, 3 acertos.
• Probabilidades de pelo menos 1 ou 2 acertos.
• Bootstrap: IC 95% da média e p-valor do ganho vs aleatório.

3.5 Procedimento de avaliação

1. Backtest 2025: treino até 2024, teste em 2025.
2. Rolling backtest: treino até o ano anterior e teste no ano seguinte, de 2000 a 2025.
3. Múltiplas janelas: repetimos o rolling para W = 10, 25, 50, 100, 200.

4. Experimentos e resultados

4.1 Backtest 2025 (holdout)

• Total de concursos: 144
• Modelo ML: média 0.604
• Baseline frequência: média 0.632
• Baseline raras: média 0.569
• Baseline aleatório: média 0.639

Interpretação: os valores ficam colados no esperado teórico (0.6), sem vantagem clara.

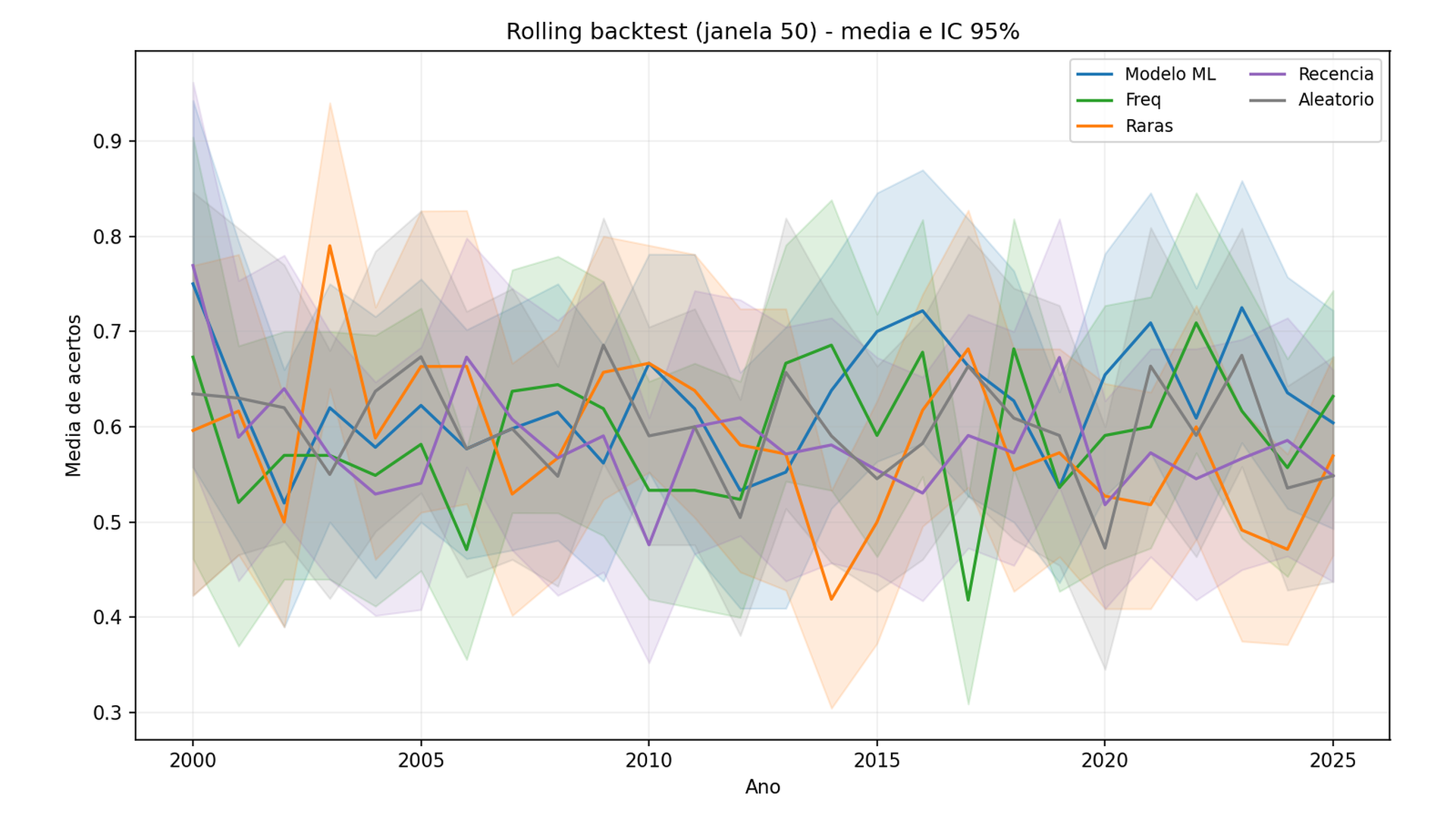
4.2 Rolling backtest (2000-2025, janela 50)

• Média anual das médias:
  • Modelo: 0.626
  • Baseline frequência: 0.592
  • Baseline raras: 0.583
  • Baseline recência: 0.584
  • Baseline aleatório: 0.599
• Modelo > aleatório: 16/26 anos
• p-valor < 0.05 (modelo vs aleatório): 1/26 anos (2020)

Interpretação: o modelo às vezes fica acima do aleatório, mas raramente com significância estatística.

4.3 Resumo por janela (média anual das médias)

• Janela 10: Modelo 0.599 | Aleatório 0.599
• Janela 25: Modelo 0.606 | Aleatório 0.599
• Janela 50: Modelo 0.626 | Aleatório 0.599
• Janela 100: Modelo 0.596 | Aleatório 0.599
• Janela 200: Modelo 0.613 | Aleatório 0.598

Interpretação: a janela 50 é o melhor caso do modelo, mas os ganhos seguem pequenos.

5. Gráficos (rolling por janela)

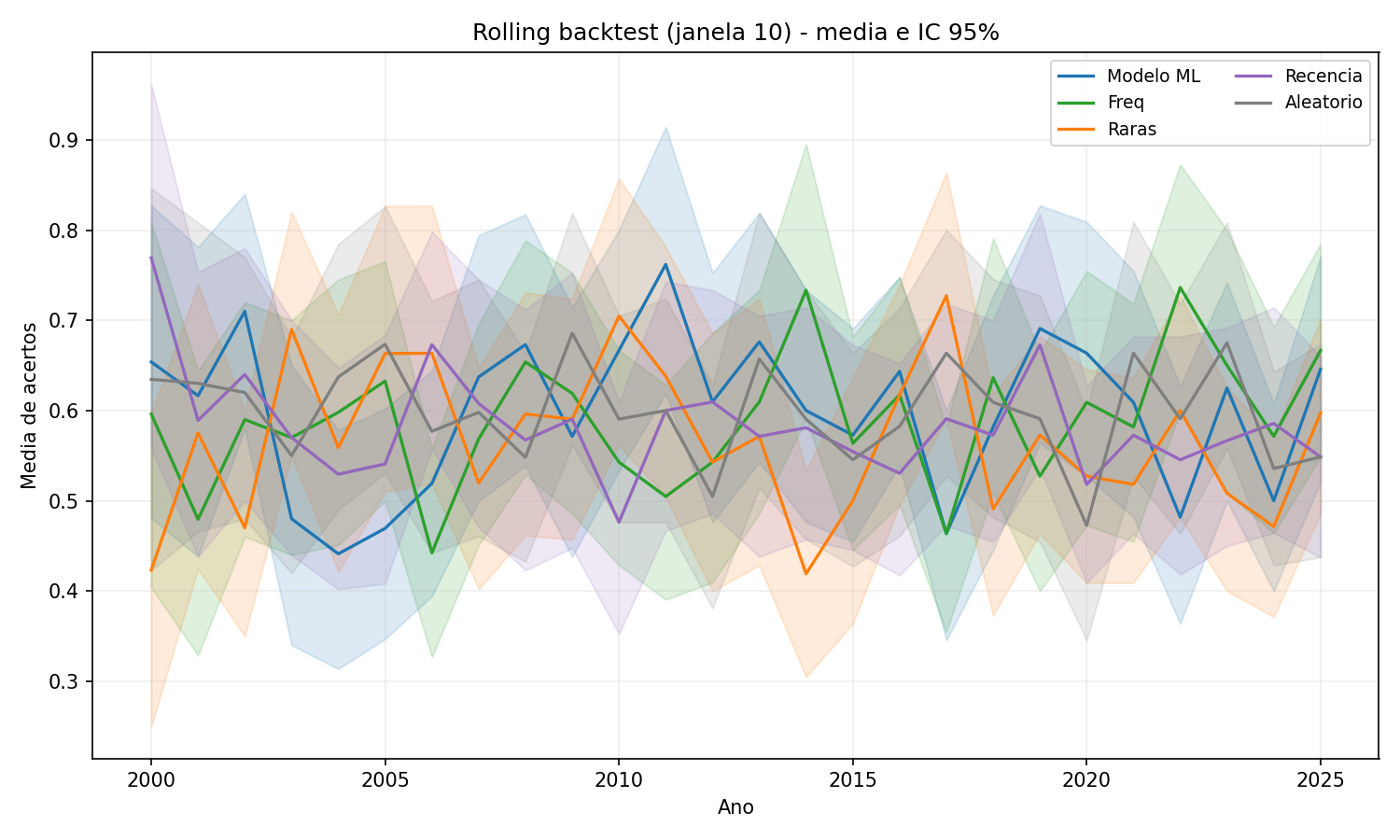Figura 1 - Janela 10 usa histórico curto, então as curvas oscilam bastante. As médias ficam muito próximas do aleatório, e os ICs 95% se sobrepõem quase o tempo todo.

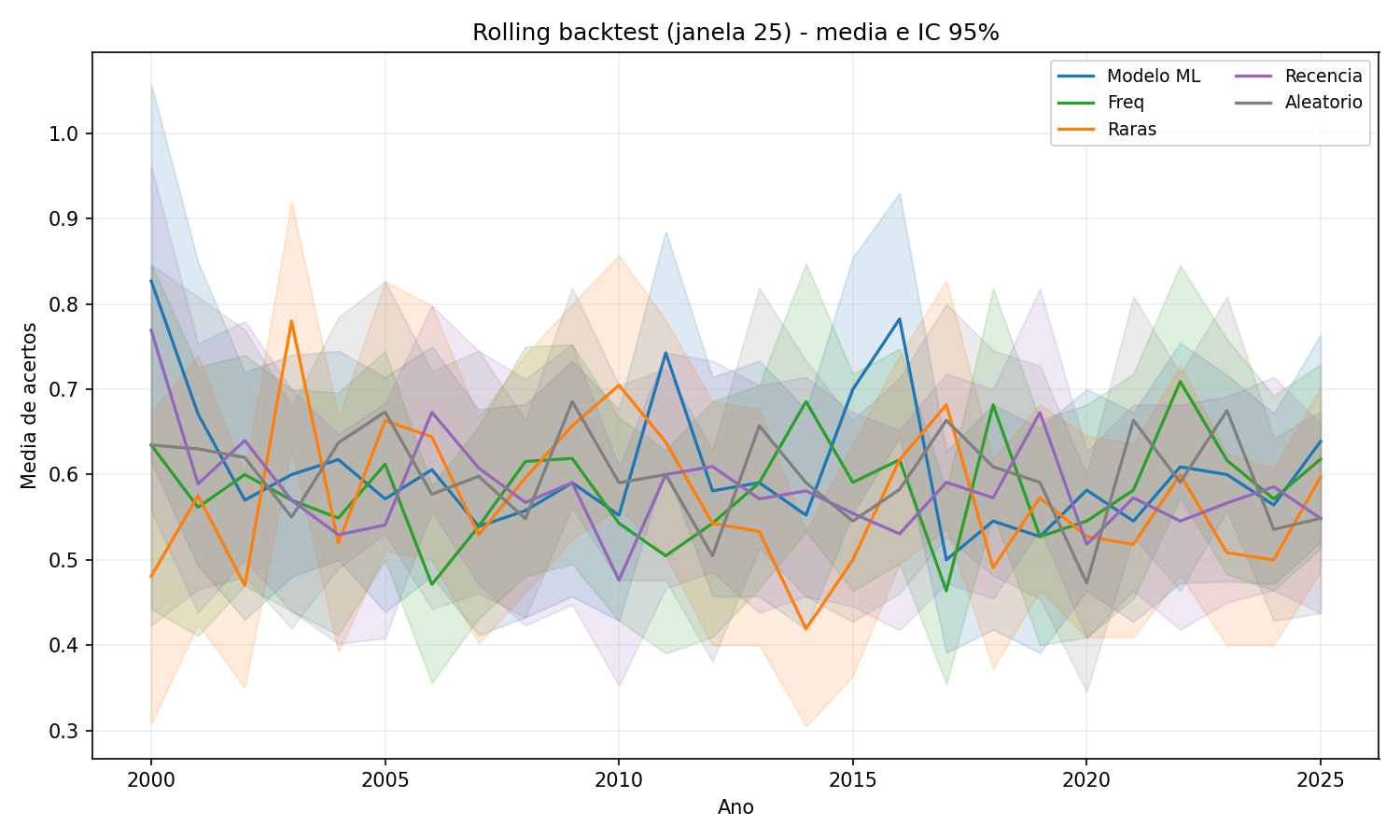Figura 2 - Janela 25 reduz parte do ruído, mas as linhas ainda se cruzam com frequência. O modelo não sustenta vantagem ano após ano.

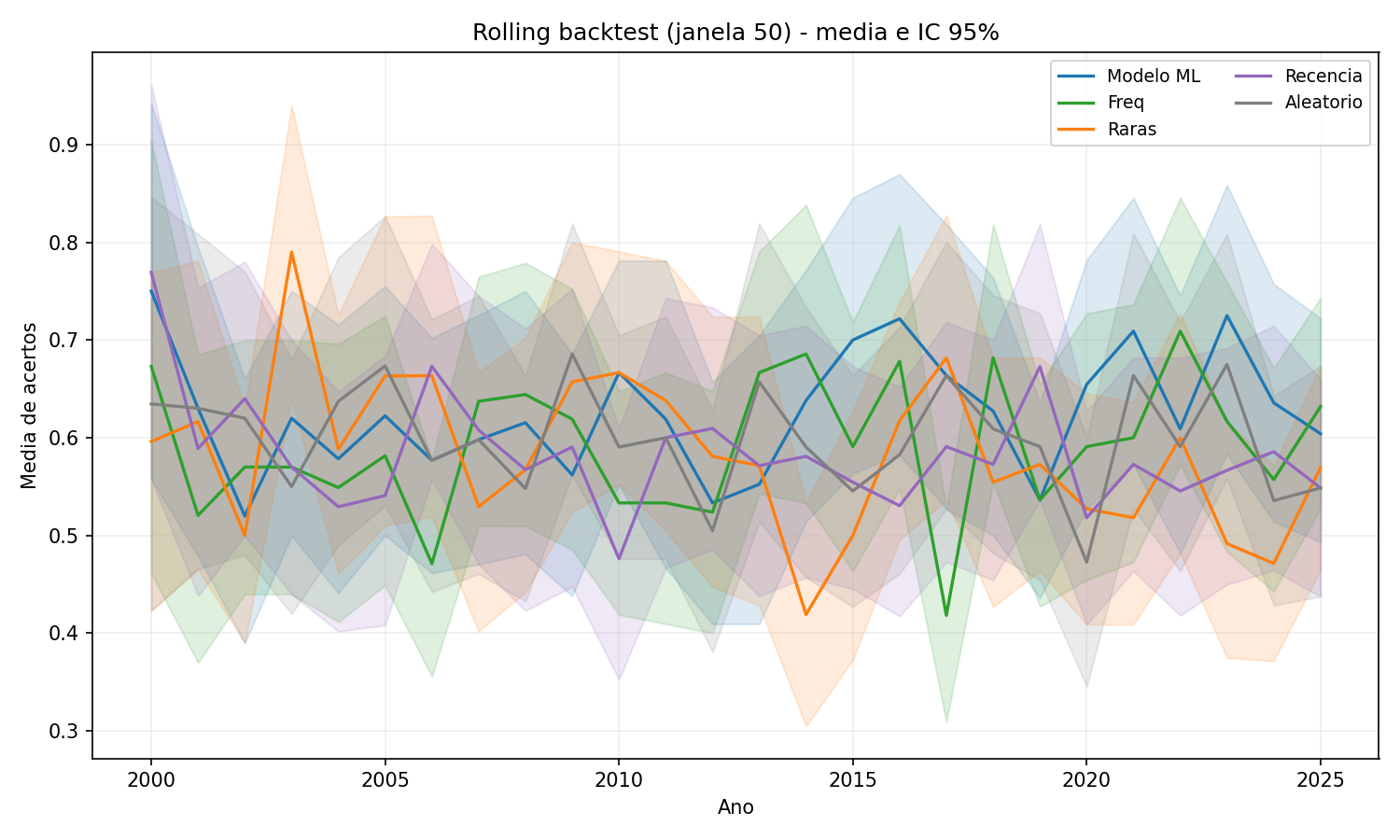Figura 3 - Janela 50 é o melhor caso do modelo em média, mas os intervalos de confiança ainda se sobrepõem com o aleatório, indicando ausência de ganho robusto.

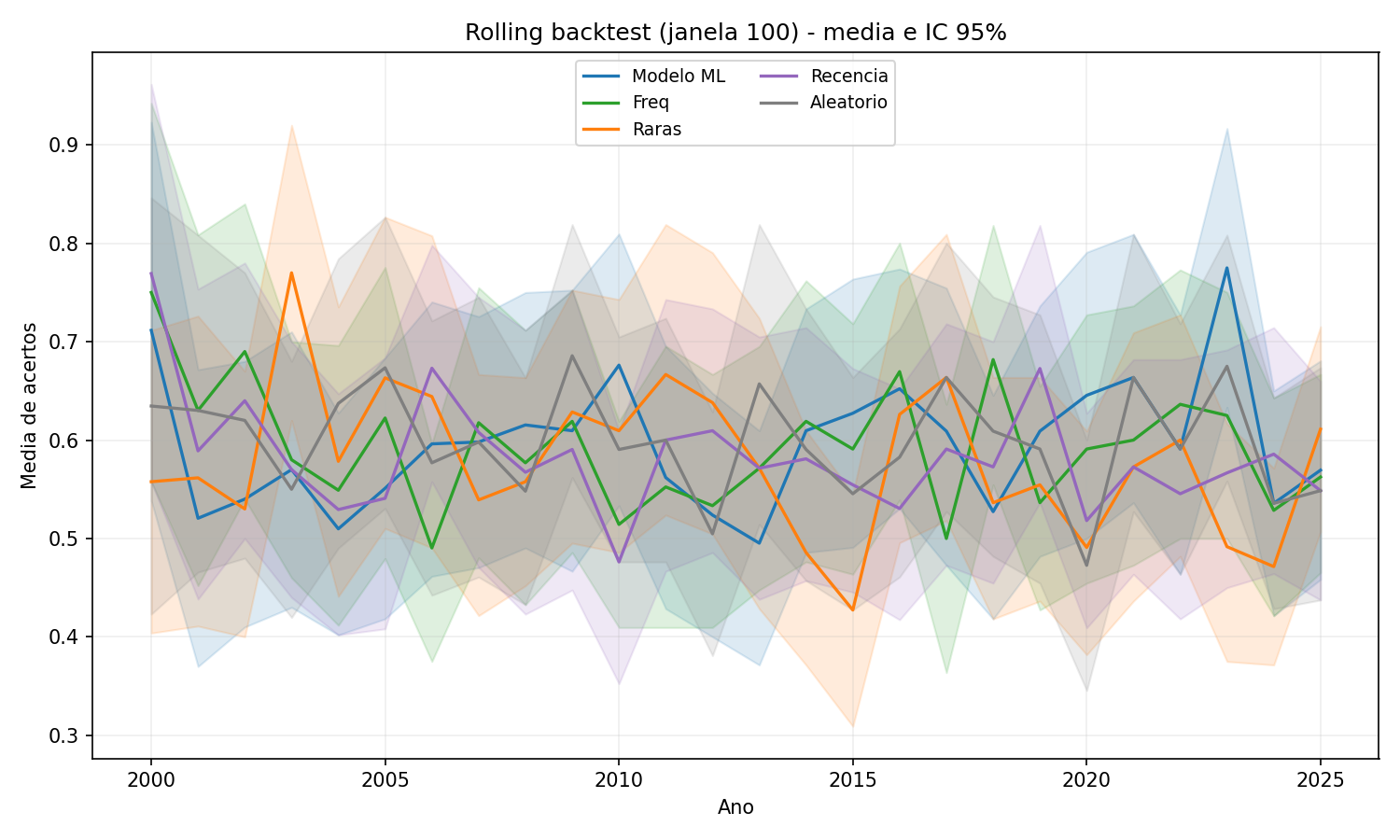Figura 4 - Janela 100 suaviza ainda mais as curvas e aproxima todos os métodos. Quando o histórico fica grande, o suposto sinal desaparece.

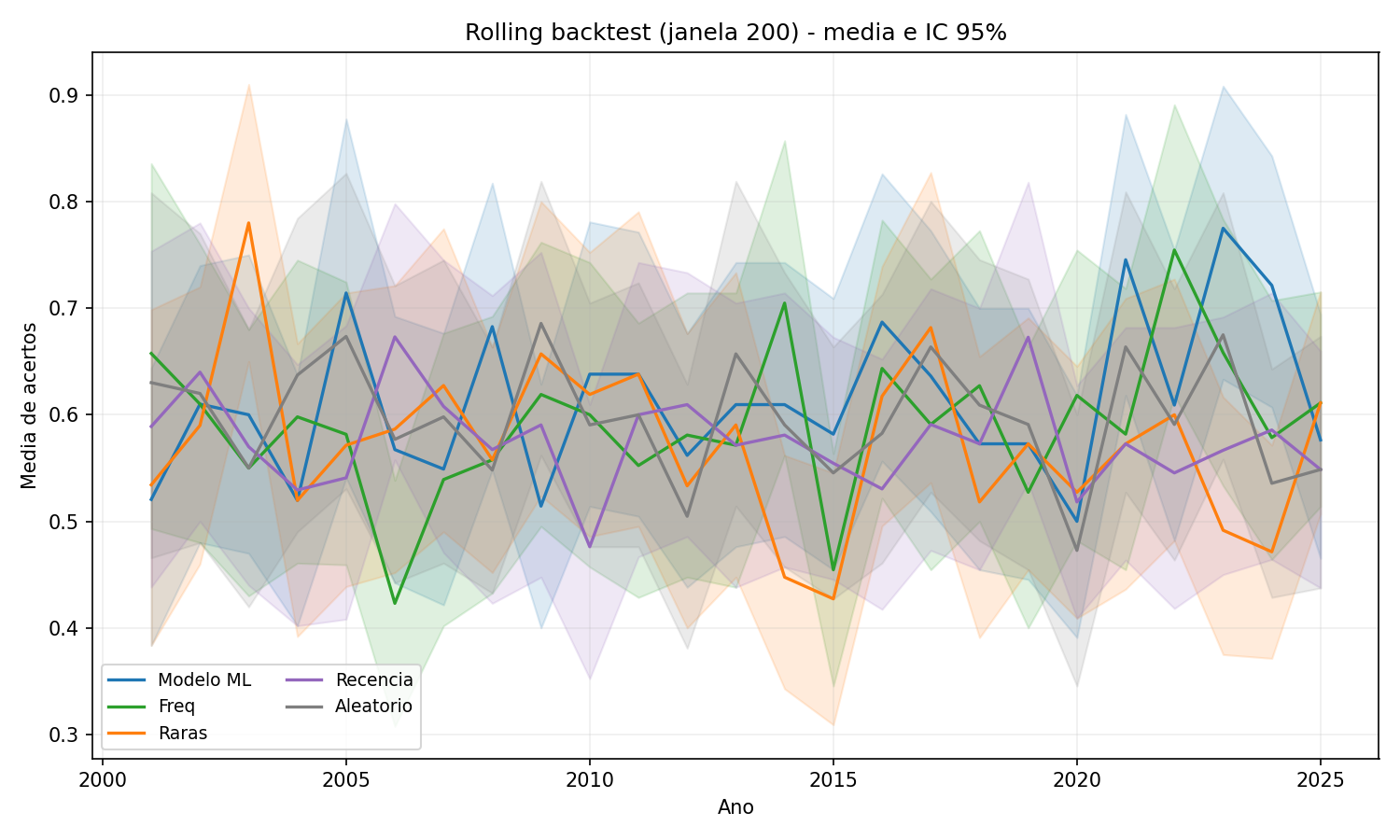Figura 5 - Janela 200 deixa as curvas mais estáveis, mas a conclusão é a mesma: nenhum método se distancia do aleatório de forma consistente.

6. Discussão

A conclusão principal não depende de um gráfico isolado, mas da interpretação do conjunto de testes. O que vemos nos resultados é o comportamento típico de um processo aleatório: médias muito próximas do esperado teórico, variação ano a ano, e ganhos ocasionais que não se sustentam.

6.1 Valor esperado e variação natural

O valor esperado de acertos para um palpite aleatório é:

Esse cálculo continua válido mesmo sem independência completa entre as dezenas, porque o valor esperado depende apenas da soma das probabilidades individuais. Em linguagem simples: escolher 6 números num universo de 60 gera, em média, menos de 1 acerto por concurso. Por isso, um método que apresenta médias entre 0.55 e 0.65 está exatamente dentro do esperado para um processo aleatório.

Um modelo probabilístico mais completo usa a distribuição hipergeométrica. Defina X como o número de acertos em um palpite aleatório. Então:

Se olharmos a média anual de acertos, o erro padrão esperado é:

Para 2025 (n=144): SE ~= 0.0586, então um IC 95% aproximado para o aleatório é 0.6 +- 0.115, isto é, [0.485, 0.715]. Esse intervalo cobre facilmente as médias observadas.

O que muda de ano para ano é a variância. Em anos com menos concursos, a média oscila mais. Em anos com mais concursos, ela se estabiliza. Os intervalos de confiança (IC 95%) capturam isso: mesmo quando o modelo parece melhor, os ICs tendem a se sobrepor ao aleatório. Isso é um sinal forte de ausência de efeito robusto.

6.2 Ganhos aparentes e o problema de múltiplos testes

Em 26 anos de rolling backtest, é natural que alguns anos apareçam acima do aleatório por pura sorte. Se você testa muitos períodos, alguns vão “parecer bons” por acaso. É por isso que o p-valor e a consistência temporal importam. No nosso caso, apenas 1 ano apresentou p-valor < 0.05 para o modelo, o que é exatamente o tipo de ocorrência esperada quando se fazem vários testes.

Em outras palavras: um ano bom não é evidência, e sim ruído estatístico. A evidência real seria um ganho pequeno, mas repetido, por vários anos e janelas de histórico diferentes.

Um jeito simples de ver isso: com 26 anos testados e alfa de 5%, esperamos cerca de 1 a 2 “falsos positivos” mesmo quando não há sinal. O ano de 2020, que apareceu com p-valor < 0.05, se encaixa exatamente nesse comportamento esperado. Ele é um “quase vencedor” estatístico, mas não um efeito real.

6.3 Por que frequência e recência parecem boas, mas falham

Dois mitos comuns em loterias são “números quentes” e “números frios”. A intuição é que o passado diz algo sobre o futuro. Mas em um processo aleatório sem memória, frequências recentes são apenas flutuações estatísticas.

Em janelas curtas, a frequência oscila muito e vira ruído. Em janelas longas, as frequências convergem para um comportamento quase uniforme. O baseline de recência sofre o mesmo problema: escolher números que “estão atrasados” apenas captura a falácia do jogador. Se não há dependência temporal, não existe motivo para um número “estar para sair”.

6.4 O papel dos baselines

Sem baselines, qualquer modelo parece promissor. Com baselines, as ilusões somem. Aqui usamos quatro referências claras: frequência, raras, recência e aleatório. O modelo ML só seria relevante se superasse o aleatório de forma consistente e, de preferência, também vencesse baselines simples.

O resultado mostra o contrário: em alguns anos o baseline aleatório é o melhor. Em outros, o baseline de frequência se sai melhor que o modelo. Isso não é um problema do algoritmo em si, mas um indício de que o problema não possui sinal útil.

6.5 Robustez: por que rolling e múltiplas janelas

Um backtest único é insuficiente. Por isso usamos rolling ano a ano e repetimos o experimento com várias janelas de histórico. Se houvesse sinal, esperaríamos ver o mesmo comportamento em diferentes tamanhos de janela. Mas os resultados mostram ganhos pequenos e instáveis. A janela 50 aparece como o melhor caso, mas mesmo assim sem consistência estatística.

Esse padrão sugere que o aparente ganho em uma janela específica é apenas uma coincidência do período, não um efeito real.

6.6 O que seria evidência forte

Para afirmar que existe previsibilidade, seria necessário observar:

1. ganho consistente contra o aleatório por vários anos consecutivos;
2. efeito semelhante em janelas diferentes;
3. intervalos de confiança separados do aleatório;
4. p-valores baixos de forma recorrente, não apenas em um ano isolado.

Nada disso aparece nos resultados.

6.7 O que este resultado ensina

Este estudo é um exemplo de “resultado negativo” bem controlado. Ele mostra que o método científico não serve apenas para confirmar hipóteses, mas para derrubá-las quando não há suporte nos dados. Em ciência de dados, isso é crucial: evitar que intuições virem narrativas falsas.

É importante lembrar: o fracasso aqui não significa que ML não funciona. Significa que ML não cria sinal onde não existe. Em problemas com estrutura temporal, dependência e variáveis explicativas reais, a análise de dados pode ser eficaz. Em loterias, não.

6.8 A objeção do “modelo simples”

Uma crítica comum é: “Regressão Logística é simples; com uma LSTM ou Transformer funcionaria”. O problema é que modelos complexos são famintos por dados e muito mais propensos a overfitting. Aqui temos 2954 concursos no total, e apenas 144 no ano de teste. Se um modelo linear não encontra nenhum sinal consistente, um modelo mais complexo tende a aumentar a variância e ajustar ruído do passado, não a revelar estrutura real.

Em termos de viés-variância: modelos profundos reduzem viés, mas aumentam variância. Sem sinal real e com pouco dado, isso piora a generalização. Em resumo: complexidade não cria previsibilidade, só aumenta a chance de decorar o passado.

7. Erros comuns que evitamos

• Leakage: uso indireto de informação do futuro.
• Cherry-picking: selecionar apenas o ano favorável.
• Sem baseline: comparar somente contra o próprio modelo.
• Overfitting: ajustar demais no passado sem validar no futuro.
• Confundir coincidência com sinal: ver padrão onde só há acaso.

8. Limitações e ameaças à validade

• Modelo simples: não exploramos arquiteturas mais complexas, mas o ganho esperado delas seria baixo dado o volume de dados e a ausência de sinal.
• Sem tuning: parâmetros foram mantidos fixos para evitar ajuste oportunista.
• Dados oficiais: assumimos consistência total da fonte.
• Múltipla comparação: vários testes aumentam chance de falso positivo.

9. Conclusão

Este estudo testou a hipótese de previsibilidade com o melhor critério possível para este contexto: avaliação temporal, baselines claros e verificação de robustez. O resultado é consistente com a teoria: não há sinal estatístico duradouro que permita superar o acaso.

Os poucos anos de “ganho” observados são compatíveis com ruído. Quando observamos janelas diferentes, os efeitos não persistem. Isso reforça a leitura correta do problema: loterias são sistemas desenhados para não oferecer estrutura aproveitável.

Chamar isso de “resultado negativo” não diminui o valor do trabalho. Pelo contrário: o método evitou conclusões erradas, expôs limites reais e mostrou como validar ideias com disciplina estatística. Em ciência de dados, saber dizer “não há sinal” é tão importante quanto encontrar um sinal verdadeiro.

Diferente da loteria, mercados financeiros apresentam estrutura, regimes e dependência temporal - e é aí que a análise de dados faz sentido.